A few years ago, I quickly pulled together an idea for an architecture competition, and the back of my mind has been occasionally turning it over ever since. The basic idea was to produce an automated shading device that could mimic a tree canopy, including the lighting effects of leaves fluttering in response to breezes, but also provide a finely-controllable range of light penetration and visibility, from fully blacked-out to nearly-full view.

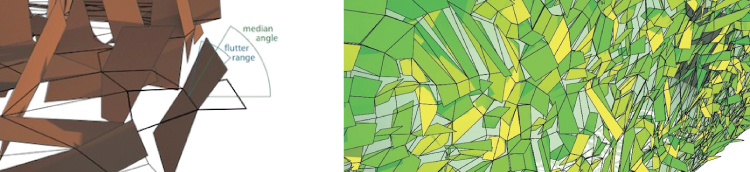
Although complex, constructing such a system is very much feasible: the 'leaves' could easily be laser-cut from one of any number of materials, and actuation and control circuitry could be routed via 'branches' through the system, which would also provide structural support. However, there are two related algorithm challenges that need to be tackled (control algorithms notwithstanding) to complete the system-design process: (1) a faster and more consistently correct algorithm to split a 2D space into many small random 4-side polygons, and (2) an algorithm for branch structure layout such that each 'leaf' (composed of two adjacent 4-side polygons) is connected to one and only one 'branch' (which overlaps with the two polygons' shared edge).

The quick-and-dirty randomized surface-splitting algorithm that I developed in RhinoScript for the architecture competition was not at all quick to run, and was rather dirty - I had to do a fair amount of manual fixing of spatially-overlapping edges (ie. intersecting lines, which should not happen) in order to produce the polygon-filled space illustration below. The challenge of the branch structure had to be punted on entirely because of time constraints (thus the wire-frame structure shown in the images above).

I have recently revisited this idea in the context of studying algorithms for the analysis of graphs (e.g. finding strongly connected components of directed graphs, finding shortest paths, etc). After a number of dead-ends, I managed to devise a surface-filling algorithm for this application that runs in linear time (relative to the number of nodes in the graph, or leaves in the shading system), and looks to be correct under all configurations, although I have not yet devised a formal proof of correctness. The algorithm is described in this IPython notebook, and its progression is illustrated in the d3 visualization below. I have not yet done enough research into other space-filling algorithms to know for sure, but I suspect this approach has its cousins, some of which are likely better. But it has been fun to figure out a way of solving a problem that has been occasionally itching the back of my mind for years.

The key insight, obvious in hindsight, was that the algorithm could be more effective and efficient if split into two parts: (1) first construct a graph with appropriate adjacencies but without considering the spatial coordinates in any detail (in the python implementation the x and y coordinates are set in a sequence of y layers); and then (2) move the nodes into appropriate positions. In the python implementation, animated below, the algorithm for stage (2) moves the nodes one at a time in the direction that would decrease their maximum edge length.

In the d3 animation at the top of this page (which constitutes the update after the initial posting), the graph produced by stage (1) is fed to a d3 force-directed graph particle simulation which spaces out the vertices, providing another way of providing stage (2) functionality. (Note that the simulation steps in this case are O(n log n) (as noted in the documentation), rather than O(n) in the case shown directly above, but the d3 version is much prettier to watch.)

Now the back of my mind can more properly turn over the related 'branches' algorithm challenge ...